Big O Notation: Explained as simply as possible
Big O can sound intimidating, but it’s actually a straightforward concept once you break it down. My goal is to explain it in the simplest way possible, focusing on what helped me grasp it best.
At its core, Big O describes how long a function takes to run or how much space it uses, expressed in terms of basic algebra.
That’s really the core idea, plain and simple! But, of course, there’s more to dive into.
Understanding Big O in theory is one thing, but explaining it effectively in an interview setting? That’s a whole different challenge. It’s not just about knowing it, it’s about clearly communicating your understanding while under pressure.
So, consider this article your go-to guide for "Learning Big O for interviews." We'll keep it practical and focused on helping you confidently explain time complexity when it matters most.
How can you sum up Big O in a few sentences?
Big O is a mathematical notation (don’t worry, high school math is all you need) that describes the worst-case scenario for how long a function takes to run. This is called time complexity. But Big O isn’t just about time—it's also used to measure space complexity, which is the worst-case amount of memory a function uses while running. The notation describes the time or space relative to input size.
In both cases, Big O provides a high-level understanding of how scalable an algorithm is as the input size grows. It answers questions like, "If the input size doubles, how much longer will it run?" or "Will this algorithm still perform well with large datasets?"
A bit more in depth
Before we go further, I'd highly recommend you check out bigocheatsheet.com. If you don't understand it fully at this point, don't worry about it. Use it as a reference, and come back to it whenever you want.
This is the site's keystone image (which if you've studied Big O at all, you've seen already):
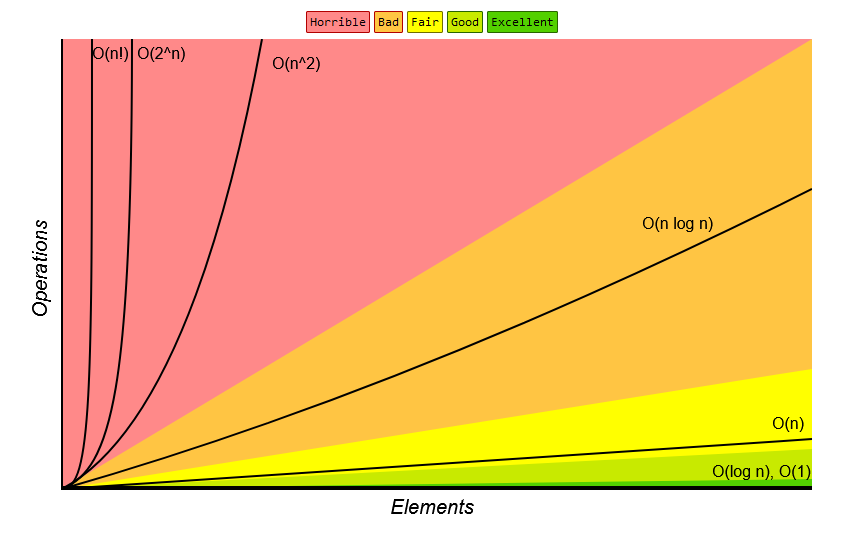
As you probably guessed:
Red = bad
Yellow = okay
Green = good
Algorithms come in all shapes and sizes. At its core, an algorithm is simply a step-by-step solution to a problem. While some algorithms can be incredibly complex, the concept itself is straightforward.
Here’s an example of an algorithm you probably already know how to do:
Imagine you’re given a list of numbers on paper and asked to find the largest one. You might scan the list from left to right, keeping track of the highest number you’ve seen so far. If you find a number larger than the current highest, you update your "highest number." That’s it, an algorithm in action!
While algorithms appear quite often in real life, they're of course most discussed in code. Here's what this algorithm might looks like in Python:
def find_largest_number(nums):
# Initialize the highest number as the first element
highest = nums[0]
# Iterate through the list to find the largest number
for num in nums:
if num > highest:
highest = num # Update highest if a larger number is found
return highestNow, how does Big O come into play? The efficiency of this simple algorithm can be represented by two values:
Time complexity: The algorithm iterates through the list from start to finish, checking each element once. Since the number of operations grows linearly with the size of the input list (n), the time complexity is O(n). In other words, for every additional element in the list, the algorithm performs one more comparison.
Space complexity: When evaluating space complexity, we focus on the additional memory the function uses during its execution, not including the memory required to store the input list. In this case, the function only uses one variable, highest, to store the largest number found. Since this is a single value and doesn’t depend on the size of the input list, the space complexity is O(1), meaning it uses a constant amount of memory regardless of the input size.
Big O values
We haven't really looked at what O(1) or O(n) means, so let's do that quickly. While there are technically an infinite number of Big O values, they are usually simplified to represent the complexity based on the input size. So you won't see O(5n), because the 5 is constant and isn't related to input size. You'll simply see this as O(n).
Here are some of the most common notations you'll see:
O(1): Constant time — The algorithm takes the same amount of time to run, regardless of the input size.
O(n): Linear time — The algorithm's runtime grows directly in proportion to the size of the input.
O(n log n): Log-linear time — The algorithm’s runtime grows faster than linear time but slower than quadratic time, commonly seen in efficient sorting algorithms like mergesort.
O(n^2): Quadratic time — The algorithm’s runtime grows exponentially as the input size increases, often seen in nested loops.
Inefficient operations can have even larger notations like O(n!) or O(2^n), where the number of operations grows exponentially as the input size increases. These complexities represent algorithms that become highly inefficient as the input grows.
For example, O(n^2) is fairly common, especially in algorithms with nested loops, such as bubble sort or selection sort. However, the main goal of Big O analysis is to evaluate your algorithm's efficiency and, where possible, find a more optimized solution that handles larger inputs more effectively.
Optimizing an Algorithm: From O(n²) to O(n)
Algorithm analysis sounds difficult, but it's not actually that difficult. It's only difficult if you don't understand the tools available to you. Anyone who has taken a formal course in Data Structures may have exposure to this, but self-taught coders might not find algorithm analysis in their learning plans.
So, let’s use a classic problem from LeetCode to analyze an algorithm and find a better solution: "Two Sum". This problem asks us to find two numbers in an array that add up to a given target. I'll show both the inefficient O(n^2) solution using a brute force approach, followed by the optimized O(n) solution using a hash map (dictionary).
Problem: Given an array of integers, find the two numbers in an array that add up the the value of target.
So, if we're given a target value of 9, we need to find the two numbers in the array that add up to 9. This could be [8,1], [6,3], etc.
Here's the inefficient O(n^2) solution, that grows exponentially more complex as the input size grows:
def two_sum_bruteforce(nums, target):
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[i] + nums[j] == target:
return [i, j]
return NoneThis solution uses two nested loops to check every pair of numbers in the list. The time complexity is O(n²) because for each number, it compares it with every other number once, resulting in n * n comparisons.
A beginner programmer might write this, and that's okay. It's technically not bad. It's readable, intuitive to understand what's happening, and solves them problem. Most will attest that nested for loops are common in production code. But, it could be better.
Here's the optimized O(n) Solution (Using a Hash Map):
def two_sum_optimized(nums, target):
seen = {} # Dictionary to store the complement of each number
for i, num in enumerate(nums):
complement = target - num
if complement in seen:
return [seen[complement], i]
seen[num] = i
return NoneIn this optimized version, there's no nested loop. Ee only iterate through the list once. For each number, we check if the complement (i.e., target - num) is already in the seen dictionary. If it is, we return the indices of the two numbers. This reduces the time complexity to O(n) because we're only iterating through the list once, and dictionary lookups are constant time.
Can Every Algorithm Be Optimized?
Not every algorithm can be optimized, no matter how much we try. While it's easy to think we can always make things faster or more efficient, some problems just have limits that can't be pushed any further. It’s kind of like trying to run faster than the speed of light, it just isn't possible within the rules.
For example, some simple sorting algorithms, like Selection Sort or Bubble Sort, have a time complexity of O(n²), meaning they take longer as the list of items grows. You might try different tricks to speed them up, but no matter what, they’ll always be slow compared to other sorting methods, like Merge Sort or Quick Sort, which run faster at O(n log n). The reason is that these simpler algorithms are fundamentally limited by how they compare each item with the others.
Then there are problems, like the Traveling Salesman Problem, that are just really tough to crack. Some problems might need to check so many possible solutions that no matter how clever we are, we can't reduce the time it takes. In these cases, we can try to find approximations (faster guesses), but we might never get to a "perfect" solution in a reasonable amount of time.
So, while it’s great to try to optimize algorithms, it’s also important to know when we’ve reached the limits. Some problems just won’t get any faster, no matter how hard we try.
What do we do if we can't optimize an algorithm?
Not every algorithm can be optimized to the point of making it fast enough for all situations. Some problems have inherent limitations, and no matter how clever we get, there’s a point where an algorithm's performance can’t be improved beyond a certain level. Think of it like trying to make a car go faster than the speed limit, no matter how much you tune it, you’ll hit a limit set by the laws of physics.
The Limits of Optimization
Let’s look at some common algorithms and their Big O complexities to illustrate this idea.
Bubble Sort: O(n²)
Bubble Sort is a classic example of a simple algorithm with poor performance. In Bubble Sort, you repeatedly loop through the list, comparing each pair of adjacent elements and swapping them if they’re in the wrong order. This process is repeated for every element in the list, which leads to a time complexity of O(n²).
No matter what we try to do, Bubble Sort will always have this O(n²) time complexity, because it has to check every pair of elements in the list. This makes it slow for large lists.
Quicksort: O(n log n)
Imagine we’re computer scientists in the early days of algorithm development. Let’s pretend Bubble Sort is the only sorting algorithm around, and we’ve reached its limit. We’ve tried every trick to make it faster, but it just won’t get any better. So, what’s our next step? We invent a new algorithm.
Quicksort works by selecting a "pivot" element, then rearranging the list so that all elements less than the pivot come before it, and all elements greater than the pivot come after it. It then recursively sorts the sublists.
Quicksort has a much better time complexity of O(n log n), which is much faster for large datasets compared to O(n²). This O(n log n) time complexity allows it to handle larger lists much more efficiently. But it comes at a cost: it uses O(log n) additional memory because of the recursion stack.
Counting Sort: O(n + k)
Quicksort is quick, as the name suggests. But we can sort even faster! Counting Sort is one such algorithm that is considered one of the fastest sorting algorithms. Instead of comparing elements, Counting Sort counts how many times each number appears and uses these counts to directly place elements in their correct positions. This makes it incredibly fast for sorting integers within a small range.
Counting Sort’s time complexity is O(n + k), where n is the number of elements in the list and k is the range of values. When the range k is small compared to n, Counting Sort can outperform algorithms like Quicksort (O(n log n)) because it avoids expensive comparisons and sorting steps. However, the trade-off is that it uses O(k) additional memory to store the counts, which can be inefficient if the range of values is large.
While Counting Sort is super efficient for certain types of data, it’s not a one-size-fits-all solution. It only works with integers or data that can be mapped to integers, and it can be quite memory-heavy if the range is large. But for the right dataset, it’s a game-changer, offering a fast and tailored solution where other algorithms might struggle.
The Trade-Off: Time vs. Space
The big question we need to ask when optimizing algorithms is, "What’s more important to us: speed or memory usage?" Here’s an example of this tradeoff:
- Quicksort runs faster than Bubble Sort because its time complexity is much better (O(n log n)), but it uses more memory due to the recursive calls.
- On the other hand, Bubble Sort uses O(1) space—it doesn’t require any extra memory beyond the input list. But, it’s much slower with its O(n²) time complexity.
This trade-off between time and space is a key part of algorithm design. Sometimes, you might be okay with using more memory if it means getting results faster, and other times, you might need to conserve memory, even if it means the algorithm runs slower.
Knowledge Necessary for Interviews
While you've already covered the essentials of Big O, there are a few more advanced concepts and nuances related to time and space complexity that are important to understand for coding interviews.
The tricky thing is, all companies decide on their own interview processes. Some will ask technical questions, some will ask you to solve Leetcode problems, some will ask really obscure things to get you thinking on your feet.
It's near impossible to remember everything about algorithms, but exposing yourself to common topics related to Data Structures and Algorithms will help you build a solid technologically literate base.
Ideally, you'll get asked questions related to the job role, but this isn't always the case. Understanding these topics, even if you'll never use them in the job role, are important for succeeding in technical interviews.
Here's an overview of some topics that may come up in interviews, and knowledge that is valuable for interviewing. Even being somewhat familiar with these topics could create talking points and help you sound more confident when discussing algorithms.
Amortized Analysis
Amortized analysis is a technique used to analyze the average time complexity of operations over a sequence of operations, rather than on a single operation. This is useful when an operation might occasionally take longer but is typically faster on average.
For example, in a dynamic array (like Python's list or Java's ArrayList), appending elements is usually O(1). However, when the array needs to resize, it may take O(n) time. Over many operations, though, the amortized time for appending is O(1), as resizing occurs infrequently.
Further Reading: Look into the amortized time complexity of operations in data structures like dynamic arrays and linked lists.
Best, Worst, and Average Case Complexity
Big O usually refers to worst-case time complexity, but sometimes you need to consider the best-case and average-case scenarios:
- Best Case: The minimum time an algorithm will take (e.g., when an array is already sorted).
- Worst Case: The maximum time the algorithm could take, typically the focus of Big O notation.
- Average Case: The expected time complexity over random inputs. Some algorithms, like quicksort, require knowledge of probability theory to calculate average-case time complexity.
Further Reading: Review how to calculate best, worst, and average case complexities for sorting algorithms like bubble sort and quicksort.
Space Complexity in Detail
Space complexity involves more than just tracking extra variables. It includes:
- Auxiliary Space: The additional memory an algorithm needs, excluding the space for the input. This includes recursion stack space and dynamically allocated memory.
- Stack vs Heap: Can you describe in detail when an algorithm uses stack vs heap? Can you describe the difference between stack and heap?
- In-Place Algorithms: Algorithms that use a constant amount of extra space, like bubble sort and heapsort, have O(1) space complexity. Can you describe the conditions for an algorithm to be O(1)?
Further Reading: Investigate the difference between auxiliary space and total space complexity, and explore in-place algorithms.
Space-Time Trade-Off
Sometimes, there’s a trade-off between time and space complexity. By using more memory, we can often reduce time complexity, and vice versa. For example, a hash table allows O(1) lookups but requires O(n) space. On the other hand, an algorithm without extra space may take longer (e.g., O(n^2)).
If you're given a specific sorting algorithm, can you describe situations when it's acceptable to use it?
Further Reading: Explore trade-offs in algorithm design, particularly in data structures like hash maps and dynamic programming approaches.
Big O Notation and Recursive Algorithms
When analyzing recursive algorithms, Big O notation becomes more complex due to recursive calls. Key points include:
- Recurrence Relations: Use techniques like the master theorem or the recursion tree method to solve time complexity for recursive algorithms. For example, a divide-and-conquer algorithm like merge sort has the recurrence relation:
T(n) = 2T(n/2) + O(n), which simplifies to O(n log n).
Further Reading: Look into recurrence relations and how to apply the master theorem for analyzing recursive algorithms.
Non-Elementary Operations
Some operations, like finding the shortest path in a graph or matrix multiplication, require advanced analysis:
- Matrix Multiplication: The standard algorithm has O(n^3) complexity, but advanced algorithms like Strassen’s reduce it to O(n^2.81).
Further Reading: Learn more about non-elementary operations like matrix multiplication, graph traversal algorithms, and their complexities.
Logarithmic and Exponential Growth
Understanding logarithmic and exponential growth is key to recognizing time complexities:
- Logarithmic Complexity (O(log n)): This occurs when each operation reduces the input size by half, as in binary search or operations on balanced binary search trees.
- Exponential Growth (O(2^n)): Algorithms with exponential time complexity, like brute-force solutions to the traveling salesman problem, are inefficient for large inputs.
Further Reading: Explore binary search, logarithmic algorithms, and the implications of exponential time complexity in algorithm design.
Big O in Practice
While Big O notation provides a theoretical measure of efficiency, real-world performance can differ due to factors like cache locality and input sizes. Optimizing an algorithm for practical use involves techniques like memoization, caching, and parallel processing.
Understand ways that algorithms are used in production code, and how to optimize them.
Further Reading: Delve into practical optimizations such as caching, memoization, and parallel computing to enhance algorithm performance in real-world scenarios.
Next Steps
If you’ve never taken a Data Structures & Algorithms course, I highly recommend you do so. There are plenty of free courses available on platforms like YouTube, Coursera, EdX, and many others. These courses offer a structured introduction to the essential concepts that every programmer needs to know.
Once you're familiar with the basics, it's time to start the Leetcode grind! While it may feel like a grind at times, it’s crucial for two main reasons. First, it provides hands-on practice with algorithmic thinking, which will make you a better programmer overall. Second, many technical interviews involve Leetcode-style questions, so mastering these types of problems can significantly improve your interview success.
While the overuse of Leetcode in interviews has it's issues, which could be a topic for another discussion, the reality is that they’re an important part of the interview process for many companies. So, putting in the time and effort to practice can make a big difference.